Plan (mathématiques)

En géométrie classique, un plan est une surface plate illimitée^[1], munie de notions d’alignement, d’angle et de distance, et dans laquelle peuvent s’inscrire des points, droites, cercles et autres figures planes usuelles. Il sert ainsi de cadre à la géométrie plane, et en particulier à la trigonométrie lorsqu’il est muni d’une orientation, et permet de représenter l’ensemble des nombres complexes.

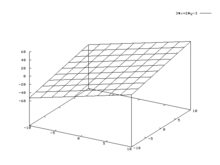
Un plan dans un espace euclidien à trois dimensions.

Un plan peut aussi se concevoir comme partie d’un espace tridimensionnel euclidien, dans lequel il permet de définir les sections planes d’un solide ou d’une autre surface. Plus généralement, un plan apparait en géométrie vectorielle et géométrie affine, comme un sous-espace de dimension 2, abstraction faite des notions d’angle et de distance. En définissant ces structures sur d’autres corps que celui des nombres réels, le concept de plan se résume à une structure d’incidence satisfaisant le théorème de Desargues.

En géométrie projective, le plan est complété par une droite à l'infini pour obtenir un plan projectif, comme le plan de Fano. Cette structure définit une géométrie non euclidienne comme dans le plan hyperbolique.

Définitions modifier

Premières approches modifier

En géométrie classique, la définition d'un plan est axiomatique et vise à idéaliser^[2]^,^[3] les représentations physiques de surfaces planes (table, tableau, feuille...). On trouve une définition axiomatique du plan chez Euclide, vers 300 ans avant Jésus-Christ, qui définit une surface comme « ce qui a longueur et largeur seulement »^[4] et précise alors dans sa définition 7 :

Une superficie plane est celle qui est également placée entre ses lignes droites.

Plusieurs siècles plus tard, Denis Henrion, dans sa traduction et commentaires des Éléments, tente d'expliciter le sens de « également placée entre ses lignes droites »^[5] indiquant que c'est une surface dont toutes les parties du milieu ne sont plus élevées ni abaissée que les extrêmes, que c'est la surface la plus courte parmi celles ayant mêmes extrêmes, que les parties du milieu y ombrage les parties extrêmes. Il explique que, si par un point quelconque d'une surface , on peut faire tourner une droite en restant dans la surface, alors cette surface est plane.

Cette même idée transparaît dans la définition d'Adrien-Marie Legendre dans ses Éléments de Géométrie^[6] (1790) :

Une surface est ce qui a longueur et largeur, sans hauteur ni épaisseur. Le plan est une surface, dans laquelle, prenant deux points à volonté et joignant ces deux points par une ligne droite, cette ligne est entièrement dans la surface.

ou bien dans cette définition de La Petite encyclopédie des mathématiques^[7] (1980) :

L'ensemble des droites issues d'un point A et coupant une droite d ne passant pas par A, ou parallèles à d forme un plan.

Repérage cartésien modifier

Au XVII^e siècle, la géométrie analytique de Descartes et Fermat décrit tous les points du plan par des couples $(x,y)$ de coordonnées. En langage mathématique contemporain, le plan est alors en bijection avec l’ensemble $\mathbb {R} ^{2}$ , de sorte que la distance entre deux points corresponde à la norme euclidienne $d((x_{1},y_{1}),(x_{2},y_{2}))={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}$ illustrant le théorème de Pythagore.

De même, en représentant l’espace comme l’ensemble $\mathbb {R} ^{3}$ des triplets $(x,y,z)$ de nombres réels, un plan est l’ensemble des solutions d’une équation cartésienne de la forme $ax+by+cz+d=0$ , où les coefficients $a,b,c$ ne sont pas tous nuls. Les plans apparaissent ainsi comme les surfaces de niveau d’une forme linéaire dans l’espace.

Présentation algébrique modifier

Le développement de l'algèbre linéaire au XIX^e siècle permet une définition du plan à l'aide du concept d'espace vectoriel et de dimension sur un corps :

Un plan (vectoriel ou affine) est un espace vectoriel (ou affine) de dimension 2.

C’est le cas, par exemple, de l’ensemble des nombres complexes, l’ensemble des fonctions affines, l’ensemble des suites satisfaisant une relation de récurrence linéaire d’ordre 2 de la forme $u_{n+2}=a_{n}u_{n+1}+b_{n}u_{n}+c_{n}$ (comme celle de la suite de Fibonacci), ou l’ensemble des solutions d’une équation différentielle linéaire d'ordre 2 de la forme $y''=a(x)y+b(x)y'+c(x)$ sur un intervalle donné.

Cette présentation implique l’existence d’un point $O$ et de deux vecteurs ${\vec {u}}$ et ${\vec {v}}$ tel que les points du plan soient les points $M$ satisfaisant une égalité vectorielle de la forme ${\overrightarrow {OM}}=a{\vec {u}}+b{\vec {v}}$ , où $a$ et $b$ décrivent tous deux le corps des scalaires. On dit alors que le triplet $(O,{\vec {u}},{\vec {v}})$ est un repère cartésien du plan, et on utilisera cette présentation dans la suite de l’article.

Le plan de la géométrie classique se réalise dans un espace affine sur le corps des nombres réels. Mais de nombreuses constructions géométriques gardent du sens sur d’autres corps, en particulier sur des corps finis.

Structure d'incidence modifier

À la fin du XIX^e siècle, après la découverte des géométries non euclidiennes, un mouvement se dessine pour axiomatiser encore davantage la géométrie en cherchant à la vider de son contenu ontologique. David Hilbert, dans son Grundlagen der Geometrie (Base de la géométrie), définit points, droites et plans de l'espace par les relations qui les unissent (les axiomes d'incidences):

Sur tout plan est situé au moins un point. Soient 3 points non alignés, il existe un et un seul plan contenant ces trois points. Si deux points (distincts) d'une droite sont situés dans un plan, la droite entière est située dans le plan. Si deux plans ont un point en commun, alors ils possèdent un autre point en commun. Il existe au moins 4 points non situés dans un même plan.

Une réduction des axiomes de Hilbert permet de fonder la géométrie plane en dehors du contexte de la géométrie dans l'espace :

Par deux points distincts passe une et une seule droite. Toute droite passe par au moins deux points. Il existe au moins trois points non alignés. Par un point extérieur à une droite $d$ , il ne passe qu'une seule droite disjointe de $d$ .

La structure d’incidence ainsi définie est satisfaite par tous les espaces affines de dimension 2 quel que soit le corps sous-jacent, mais aussi par d’autres structures comme le plan de Moulton.

Hilbert identifie que le théorème de Desargues de la géométrie classique se déduit d’autres axiomes mais pas de ceux d’incidence dans le plan, alors qu’il se formule uniquement en termes d’incidence. En l’introduisant comme axiome supplémentaire, il caractérise en fait tous les espaces affines de dimension 2. Et en le remplaçant par le théorème de Pappus, on obtient une caractérisation de tous les espaces affines sur des corps commutatifs.

Relations entre droites et plans modifier

Position relative modifier

Deux plans modifier

Dans un espace affine de dimension 3, il n'existe que deux positions relatives de deux plans :

ils peuvent être parallèles, autrement dit de même direction, ce qui recouvre deux cas : les deux plans sont confondus ou ils sont disjoints (et qualifiés de strictement parallèles) ;
ils peuvent être sécants : leur intersection est alors une droite.

Cette disjonction est particulière à l’espace tridimensionnel. En dimension plus grande, deux plans peuvent avoir un seul point d’intersection, ou être disjoints sans être parallèles.

La direction est facile à comparer à partir des équations cartésiennes :

Étant donné deux plans associés respectivement aux équations $ax+by+cz+d=0$ et $a'x+b'y+c'z+d'=0$ , les deux plans sont parallèles si et seulement si les vecteurs $(a,b,c)$ et $(a',b',c')$ sont colinéaires.

Ces vecteurs sont respectivement des vecteurs normaux aux plans dans une base orthogonale, ou encodent dans la base duale des formes linéaires dont les plans sont des surfaces de niveau.

Droite et plan modifier

Étant donné un plan de l’espace, une droite de cet espace peut être :

incluse dans le plan ;
sécante en un point ;
disjointe du plan, et dans ce cas elle est strictement parallèle au plan.

L’inclusion dans un espace affine de plus grande dimension ne fournit pas d’autre position relative d’une droite et d’un plan.

Propriétés modifier

Le théorème du toit stipule que si une droite d’un plan est parallèle à une droite d’un autre plan sécant au premier, alors ces droites sont parallèles à l’intersection des deux plans.

Trois plans sécants deux à deux ont des droites d’intersection qui sont nécessairement toutes parallèles ou concourantes.

Angle modifier

Dans l’espace tridimensionnel euclidien, le produit scalaire permet de définir l’angle entre deux vecteurs non nuls. Étant donné deux vecteurs non colinéaires ${\vec {u}},{\vec {v}}$ d’un plan, le produit vectoriel montre l’existence d’un vecteur ${\vec {n}}$ orthogonal à ${\vec {u}}$ et ${\vec {v}}$ (et donc à tout autre vecteur reliant deux points du plan) qualifié de vecteur normal au plan. Ce vecteur est unique à multiplication près par un scalaire.

Deux plans sécants délimitent des dièdres dont l’angle varie entre l’angle nul et l’angle plat, et qui correspond à l’angle entre leurs vecteurs normaux. Si ces vecteurs normaux sont eux-mêmes orthogonaux, les plans sont dits perpendiculaires. Ils ne sont pas dits orthogonaux, car il existe des vecteurs non nuls représentés à la fois dans l’un et dans l’autre (par exemple, des vecteurs dirigeant leur intersection dans le cas de deux plans sécants).

Distance modifier

La distance entre deux plans, ou entre un plan et une droite, est la distance minimale entre un point de l’un et un point de l’autre. Ce minimum vaut 0 si les deux ensembles sont d’intersection non vide, et est atteint le long de segment orthogonaux aux deux ensembles dans le cas contraire.

Utilisations modifier

Représentation de relation entre deux variables modifier

Le plan est le support de représentation visuelle et permet d’apprécier une relation entre deux variables numériques.

Si chaque valeur de la première variable ne correspond qu’à une valeur (au plus) de la seconde, la relation est dite fonctionnelle, et le graphe de la relation est une courbe représentative de la fonction.

Lorsque les deux variables sont décrites par un échantillon statistique, la relation est représentée par un nuage de points.

Lorsque les deux variables sont elles-mêmes fonctions d’une variable tierce, en particulier d’une variable temporelle, leur relation est illustrée par une trajectoire, éventuellement obtenue par une équation différentielle. En particulier, l’étude des relations entre l’évolution d’une grandeur et sa dérivée temporelle donne lieu à la représentation d’un portrait de phase.

Symétrie modifier

Une symétrie (orthogonale) par rapport à un plan $P$ est une transformation géométrique qui à tout point $M$ du plan associe l’unique point $M'$ tel que le segment $[M M']$ soit orthogonal au plan en son milieu.

La composée de deux symétries par rapport à deux plans sécants est une rotation autour de leur droite d’intersection, d’angle le double de l’angle dièdre.

La composée de deux symétries par rapport à deux plans parallèles est une translation d’un vecteur normal aux deux plans et de norme le double de la distance entre les plans.

Une telle symétrie est caractéristique des espèces animales bilatères.

Projection modifier

Une projection (affine) sur un plan, parallèlement à une droite $d$ sécante au plan, est une transformation géométrique qui associe à tout point $M$ l’unique point d’intersection entre le plan et la parallèle à $d$ passant par $M$ . Si la droite est orthogonale au plan, on parle alors de projection orthogonale.

Une telle projection idéalise le phénomène de l’ombre sur un support plan dans le cas d’un éclairage à l’infini (qui est une bonne approximation de l’éclairage du Soleil). La projection affine sur un plan régit aussi la représentation en perspective cavalière. On l’utilise également en plus grande dimension pour visualiser un nuage de données, notamment à l’aide de l’analyse en composantes principales.

Section modifier

Une section plane d’une figure de l’espace est simplement l’intersection de cette figure avec un plan. Cette notion permet de visualiser des structures mathématiques ou concrètes comme en architecture, en physique, chimie et biologie, notamment avec l’utilisation de scanner tridimensionnel.

Changement de représentation modifier

Dans un cadre affine modifier

Les axiomes d’incidence de Hilbert mettent en évidence différentes caractérisations d’un plan dans un espace affine. Il existe un unique plan :

contenant trois points non alignés ;
contenant une droite et un point n'appartenant pas à cette droite ;
contenant deux droites sécantes ;
contenant deux droites non confondues et parallèles.

La première caractérisation permet d’obtenir simplement chacune des suivantes, et réciproquement.

À partir de trois point $A$ , $B$ , $C$ non alignés, on peut définir un repère $(A,{\overrightarrow {AB}},{\overrightarrow {AC}})$ . Réciproquement, tout repère peut s’écrire sous cette forme.

Étant donné un repère $(A,{\vec {u}},{\vec {v}})$ du plan, on obtient une représentation paramétrique de la forme ${\overrightarrow {OM}}=\lambda {\vec {u}}+\mu {\vec {v}}$ . En dimension 3, si l’on note $A(a_{1},a_{2},a_{3})$ , ${\vec {u}}=(u_{1},u_{2},u_{3})$ et ${\vec {v}}=(v_{1},v_{2},v_{3})$ , on obtient les équations paramétriques ${\begin{cases}x=a_{1}+\lambda u_{1}+\mu v_{1}\\y=a_{2}+\lambda u_{2}+\mu v_{2}\\z=a_{3}+\lambda u_{3}+\mu v_{3}\end{cases}}$ avec $(\lambda ,\mu )\in \mathbb {R} ^{2}$ . Réciproquement, toute représentation paramétrique affine permet de retrouver les coordonnées du point origine (en annulant les paramètres) et des deux vecteurs directeurs (facteurs des paramètres dans chacune des trois équations).

Enfin, à partir d’un repère $(A,{\vec {u}},{\vec {v}})$ du plan dans l’espace et un point générique $M(x,y,z)$ , l’appartenance du point au plan est caractérisée par l’annulation du produit mixte de vecteurs ${\overrightarrow {AM}}$ , ${\vec {u}}$ , ${\vec {v}}$ , lequel mesure le défaut de coplanarité.

0=[{\vec {u}},{\vec {v}},{\overrightarrow {AM}}]=[{\vec {u}},{\vec {v}},{\overrightarrow {OM}}]-[{\vec {u}},{\vec {v}},{\overrightarrow {OA}}]

, avec

[{\vec {u}},{\vec {v}},{\overrightarrow {OM}}]={\begin{vmatrix}u_{1}&&v_{1}&&x\\u_{2}&&v_{2}&&y\\u_{3}&&v_{3}&&z\end{vmatrix}}=\underbrace {(u_{2}v_{3}-u_{3}v_{2})} _{a}x+\underbrace {(u_{3}v_{1}-u_{1}v_{3})} _{b}y+\underbrace {(u_{1}v_{2}-u_{2}v_{1})} _{c}z

, et de même,

-[{\vec {u}},{\vec {v}},{\overrightarrow {OA}}]=\underbrace {-(aa_{1}+ba_{2}+ca_{3})} _{d}.

Ces 4 facteurs notés $a,b,c,d$ définissent alors l’équation cartésienne $ax+by+cz+d=0$ .

Réciproquement, à partir d’une équation cartésienne s’écrivant $ax+by+cz+d=0$ avec $a,b,c$ non tous nuls, on peut choisir un point solution évidente (par exemple en choisissant une coordonnée associée à un coefficient non nul, en annulant les deux autres coordonnées, et en résolvant l’équation du premier degré restante), puis on détermine une base $({\vec {u}},{\vec {v}})$ du sous-espace vectoriel d’équation $ax+by+cz=0$ dans $\mathbb {R} ^{3}$ .

Dans un cadre tridimensionnel euclidien modifier

Les caractérisations suivantes reposent sur les notions de distance et d’angle (en particulier d’orthogonalité) qui viennent de la structure euclidienne de l’espace en géométrie classique.

Étant donné un point $A$ et un vecteur ${\vec {n}}$ non nul, il existe un unique plan passant par $A$ et orthogonal à ${\vec {n}}$ , appelé le vecteur normal.

Cette caractérisation d’un plan s’obtient très facilement à partir d’un repère $(A,{\vec {u}},{\vec {v}})$ du plan, en utilisant le produit vectoriel ${\vec {n}}={\vec {u}}\wedge {\vec {v}}$ .

Réciproquement, étant donné un point $A(x_{A},y_{A},z_{A})$ et un vecteur normal ${\vec {n}}=(a,b,c)$ , on trouve facilement une équation cartésienne $a(x-x_{A})+b(y-y_{A})+c(z-z_{A})=0$ .

D’autres caractérisations se ramènent au choix d’un point et d’un vecteur normal :

Étant donné deux points $A$ et $B$ distincts de l’espace, il existe un unique plan qui est le lieu des points équidistants de $A$ et $B$ , et appelé plan médiateur du segment $[A B]$ .

Étant donné deux droites disjointes et non parallèles, il existe un unique plan qui soit à la même distance de tous les points des deux droites.

Étant donné un point $A$ et deux plans $P$ et $P'$ non parallèles dans l’espace, il existe un unique plan passant par $A$ et perpendiculaire à $P$ et $P'$ .

Géométrie vectorielle modifier

Un plan est un sous-espace de dimension 2 d'un espace vectoriel sur un corps commutatif $\mathbb {K}$ . On parle aussi dans ce cas d'un plan vectoriel.

Un plan est toujours engendré par deux vecteurs $v$ et $w$ non colinéaires. De la sorte, $x$ est un vecteur du plan si et seulement s'il est combinaison linéaire de $v$ et $w$ , à coefficients dans $\mathbb {K}$ . Si $V$ est de dimension finie $n$ , on peut aussi définir un plan par $n-2$ formes linéaires indépendantes s'annulant sur tous les vecteurs du plan. Il est particulièrement intéressant de disposer de cette dernière caractérisation, si on veut, par exemple, déterminer les points d'intersection du plan et d'un autre objet, par exemple une courbe ou une surface.

Approche analytique en dimension 3 modifier

Dans le cas où l'espace $V$ est de dimension 3, il suffit d'une seule forme linéaire pour définir un plan. Connaissant deux vecteurs $v$ et $w$ qui l'engendrent, de coordonnées

{\begin{pmatrix}v_{1}\\v_{2}\\v_{3}\end{pmatrix}}\quad {\text{et}}\quad {\begin{pmatrix}w_{1}\\w_{2}\\w_{3}\end{pmatrix}},

il est utile de savoir fabriquer une forme linéaire donnant l'équation du plan. Le produit mixte de $v$ , $w$ et $z$ est nul si et seulement si $z$ appartient au plan engendré par $v$ et $w$ . Ce produit mixte s'écrit

[v,w,z]=(v\times w)\cdot z=z_{1}(v_{2}w_{3}-v_{3}w_{2})+z_{2}(v_{3}w_{1}-v_{1}w_{3})+z_{3}(v_{1}w_{2}-v_{2}w_{1}).

On a ainsi obtenu la forme linéaire désirée.

Réciproquement, si on possède une forme linéaire $z\mapsto a_{1}z_{1}+a_{2}z_{2}+a_{3}z_{3}$ définissant un plan, on peut trouver aisément deux vecteurs engendrant ce plan à partir de la forme linéaire. Il existe forcément un coefficient non nul parmi $a_{1},a_{2}$ et $a_{3}$ . Disons que ce coefficient est $a_{2}$ . On peut alors réécrire l'équation du plan sous la forme

z_{2}=-(a_{1}z_{1}+a_{3}z_{3})/a_{2}.

Alors en substituant au couple $(z_{1},z_{3})$ les couples indépendants $(1,0)$ et $(0,1)$ , on obtient deux vecteurs

{\begin{pmatrix}1\\-a_{1}/a_{2}\\0\end{pmatrix}}\quad {\text{et}}\quad {\begin{pmatrix}0\\-a_{3}/a_{2}\\1\end{pmatrix}},

qui sont forcément indépendants puisque leurs projections respectives sur le plan des $z_{1},z_{3}$ par rapport à l'axe des $z_{2}$ sont des vecteurs indépendants.

Généralisation en dimension plus élevée modifier

Supposons qu'on ait dans un espace de dimension $n$ deux vecteurs $v$ et $w$ indépendants. Comment trouver $n-2$ formes linéaires indépendantes donnant les équations du plan? Cela revient à chercher une base de solutions du système linéaire

{\begin{aligned}&\sum _{i=1}^{n}v_{i}x_{i}=0,\\&\sum _{i=1}^{n}w_{i}x_{i}=0.\end{aligned}}

Pour ce faire, on sélectionne deux indices $p$ et $q$ tels que les couples $(v_{p},v_{q})$ et $(w_{p},w_{q})$ soient linéairement indépendants. Géométriquement, cela revient à sélectionner un plan de coordonnées tel que les projections respectives de $v$ et $w$ sur ce plan, parallèlement au sous-espaces $\{z:z_{p}=z_{q}=0\}$ soient indépendantes. Un tel plan existe toujours parce que $v$ et $w$ sont indépendants. Une fois ceci fait, on réécrit le système précédent sous la forme

{\begin{aligned}v_{p}x_{p}+v_{q}x_{q}&=-\sum _{i\neq p,q}v_{i}x_{i},\\w_{p}x_{p}+w_{q}x_{q}&=-\sum _{i\neq p,q}w_{i}x_{i}.\end{aligned}}

La solution de ce système linéaire est obtenue par les méthodes classiques. Pour obtenir une base de l'espace des solutions, il suffira de substituer à la suite à $n-2$ éléments $(x_{i})_{i\neq p,q}$ les éléments de la base canonique de l'espace vectoriel $\mathbb {K} ^{n-2}$ , c'est-à-dire

(1,0,0,\dots ,0),(0,1,0,\dots ,0),(0,0,1,\dots ,0),\dots ,(0,0,0,\dots ,1)

.

Réciproquement, $n-2$ formes linéaires indépendantes $\ell _{j}$ étant données, on trouve deux vecteurs indépendants dans le plan défini comme ensemble des points où s'annulent ces formes linéaires, en trouvant une base de l'ensemble des solutions du système $\ell _{1}(z)=0,\ell _{2}(z)=0,\dots ,\ell _{n-2}(z)=0.$ En pratique, la meilleure manière de procéder est de mettre la matrice $L$ du système sous forme échelonnée, moyennant d'éventuelles permutations sur les colonnes. Comme $M$ est de rang $n-2$ , cet algorithme fournira $n-2$ variables par rapport auxquelles on résoudra, et deux variables indépendantes à mettre dans le second membre. La résolution est alors rapide. Il faut absolument éviter les formules de Cramer pour détecter les indices des variables par rapport auxquelles on résout : il faudrait calculer $n(n-1)/2$ déterminants $(n-2)\times (n-2)$ , pour un nombre total d'opérations de l'ordre de $n^{4}$ , si on calcule les déterminants par algorithme de Gauss-Jordan, alors que le passage sous forme échelon permet de conclure pour un nombre d'opérations de l'ordre de $n^{3}$ .

Notes et références modifier

↑ Stella Baruk, « Plan » dans le Dictionnaire de mathématiques élémentaires, Éditions du Seuil, Paris 1995.
↑ La géométrie - histoire et épistémologie, chap 27: élaboration d'objets idéaux dans Culturemath.ens.fr
↑ Thomas Hausberger, « Repères historiques et épistémologiques sur les Géométries non euclidiennes », Irem de Montpellier - group Mathématiques et philosophie, 2015
↑ Euclide, Éléments, Livre 1, définition 7
↑ D. Henrion, Les quinze livres des éléments géométriques d'Euclide : plus le livre des donnez du mesme Euclide aussi traduict en françois par ledit Henrion, et imprimé de son vivant, livre Premier, définition 7.
↑ Adrien Marie Legendre, Eléménts de géométrie - Livre Premier. Définitions 5 et 6, 1840
↑ Collectif (dir. W. Gellert, H. Küstner, M. Hellwich, H. Kästner) (trad. sous la direction de Jacques-Louis Lions, professeur au Collège de France), Petite encyclopédie des mathématiques [« Kleine Enzyklopädie der Mathematik »], Paris, Didier, 1997 (1^re éd. 1980), 896 p. (ISBN 978-2-278-03526-7), p. 201.

Voir aussi modifier

Articles connexes modifier

Liens externes modifier

Adrien Javary, Traité de géométrie descriptive, 1881 (sur Gallica) : La ligne droite, le plan, les polyèdres
Résolution des difficultés d'arithmétique et de géométrie planaire (Manuscrit arabe, XV^e siècle)

Portail de la géométrie

[1] Stella Baruk, « Plan » dans le Dictionnaire de mathématiques élémentaires, Éditions du Seuil, Paris 1995.

[2] La géométrie - histoire et épistémologie, chap 27: élaboration d'objets idéaux dans Culturemath.ens.fr

[3] Thomas Hausberger, « Repères historiques et épistémologiques sur les Géométries non euclidiennes », Irem de Montpellier - group Mathématiques et philosophie, 2015

[4] Euclide, Éléments, Livre 1, définition 7

[5] D. Henrion, Les quinze livres des éléments géométriques d'Euclide : plus le livre des donnez du mesme Euclide aussi traduict en françois par ledit Henrion, et imprimé de son vivant, livre Premier, définition 7.

[6] Adrien Marie Legendre, Eléménts de géométrie - Livre Premier. Définitions 5 et 6, 1840

[7] Collectif (dir. W. Gellert, H. Küstner, M. Hellwich, H. Kästner) (trad. sous la direction de Jacques-Louis Lions, professeur au Collège de France), Petite encyclopédie des mathématiques [« Kleine Enzyklopädie der Mathematik »], Paris, Didier, 1997 (1^re éd. 1980), 896 p. (ISBN 978-2-278-03526-7), p. 201.

[1]

[2]

[3]

[4]

[5]

[6]

[7]