Wikipédia:Sélection/Mathématiques
Théorème de Pythagore Le théorème de Pythagore est un théorème de géométrie euclidienne qui met en relation les longueurs des côtés dans un triangle rectangle : le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés. Ce théorème permet notamment de calculer l’une de ces longueurs à partir des deux autres. Il est nommé d’après Pythagore de Samos, philosophe de la Grèce antique. Cependant le résultat était connu plus de mille ans auparavant en Mésopotamie, et, même si les mathématiciens grecs en connaissaient probablement une démonstration avant Euclide, auteur dans ses Éléments de la plus ancienne qui nous soit parvenue, rien ne permet de l'attribuer à Pythagore. Par ailleurs le résultat a vraisemblablement été découvert indépendamment dans plusieurs autres cultures. Les premières démonstrations historiques reposent en général sur des méthodes de calcul d’aire par découpage et déplacement de figures géométriques. Inversement, la conception moderne de la géométrie euclidienne est fondée sur une notion de distance qui est définie pour respecter ce théorème. Divers autres énoncés généralisent le théorème à des triangles quelconques, à des figures de plus grande dimension telles que les tétraèdres, ou en géométrie non euclidienne comme à la surface d’une sphère. |
Théorème de Thalès Le théorème de Thalès est un théorème de géométrie, attribué selon la légende au mathématicien et philosophe grec Thalès de Milet ; en réalité Thalès s'est davantage intéressé aux angles opposés dans des droites sécantes, aux triangles isocèles et aux cercles circonscrits. Cette propriété de proportionnalité était connue des Babyloniens. Mais la première démonstration de ce théorème est attribuée à Euclide qui la présente dans ses Éléments (proposition 2 du livre VI) : il le démontre par proportionnalité d'aires de triangles de hauteur égale. Selon la légende, une application a été de calculer la hauteur des pyramides d'Égypte en mesurant la longueur de l'ombre au sol de chaque pyramide, et la longueur de l'ombre d'un bâton de hauteur donnée. |
Théorème d'Al-Kashi Le théorème d'Al-Kashi est un théorème de géométrie du triangle couramment utilisé en trigonométrie. Il généralise le théorème de Pythagore aux triangles non rectangles : il relie le troisième côté d'un triangle aux deux premiers ainsi qu'au cosinus de l'angle formé par ces deux côtés. Soit un triangle ABC, dans lequel on utilise les notations usuelles exposées sur la Fig. 1 : d'une part α, β et γ pour les angles et, d'autre part, a, b et c pour les côtés respectivement opposés à ces angles. Alors, le théorème d'al-Kashi stipule que : Dans la plupart des autres langues, ce théorème est connu sous le nom de loi des cosinus, appellation toutefois relativement tardive. En français, cependant, il porte le nom du mathématicien perse Ghiyath al-Kashi qui unifia les résultats de ses prédécesseurs. Lire l’article |
Nombre réel En mathématiques, les nombres réels peuvent très informellement être conçus comme tous les nombres associés à des longueurs ou des grandeurs physiques. Ce sont les nombres, qu’ils soient positifs, négatifs ou nuls, ayant une représentation décimale finie ou infinie. Autrement dit, ce sont les rationnels (qui peuvent s’écrire sous forme de fraction) complétés par les nombres dont la représentation décimale est infinie non périodique, tels la racine carrée de 2 et π. Ces derniers sont appelés nombres irrationnels. Parmi les nombres réels on distingue également les nombres algébriques et les nombres transcendants. Le terme de nombre réel apparaît pour la première fois chez Cantor en 1883 dans ses publications sur les fondements de la théorie des ensembles. C’est un rétronyme, donné en réponse à la découverte des nombres imaginaires. Les nombres réels sont au centre de la discipline mathématique de l’analyse réelle, à laquelle ils doivent une grande part de leur histoire. |
Fonction trigonométrique En mathématiques, les fonctions trigonométriques sont des fonctions d’angle importantes pour étudier les triangles et modéliser des phénomènes périodiques. Elles peuvent être définies comme rapports de deux longueurs des côtés d’un triangle contenant l’angle, ou, plus généralement, par les rapports des coordonnées de points du cercle trigonométrique, ou, plus généralement encore, comme somme d’une série entière. Il y a six fonctions trigonométriques circulaires de base :
Le sinus, le cosinus et la tangente sont de loin les plus importantes. Lire l’article |
Déterminant (mathématiques) Initialement introduit en algèbre pour déterminer le nombre de solutions d’un système d’équations linéaires, le déterminant se révèle un outil très puissant dans de nombreux domaines (étude d’endomorphisme, recherche de valeurs propres, calcul différentiel). C'est ainsi qu’on définit le déterminant d’un système d’équations, le déterminant d’un endomorphisme ou le déterminant d’un système de vecteurs. Comme pour de nombreuses opérations, le déterminant peut être défini par une collection de propriétés (axiomes) qu’on résume par le terme « forme n-linéaire alternée ». Cette définition permet d’en faire une étude théorique complète et d’élargir encore ses champs d’applications. Le déterminant a un fort contenu géométrique : il généralise les notions d'aire d'un parallélogramme dans le plan euclidien ou de volume d'un parallélépipède dans l'espace euclidien. Il donne également un sens général à la notion d'orientation. |
Variété (géométrie) Une variété est un espace topologique abstrait, construit par recollement d'autres espaces simples. Comme les enfants s'amusent à construire avec du papier des tétraèdres, des cubes et autres polyèdres en dessinant la figure d'un patron sur une feuille blanche, en découpant convenablement les bords, en pliant et en recollant, les mathématiciens obtiennent un cercle en repliant un segment sur lui-même, un cylindre ou un cône en repliant une bande plane sur elle-même. Un autre exemple classique est le ruban de Möbius illustré ci-contre (en toute rigueur exemple de variété à bord). Il est également possible de rajouter des anses à une sphère. Parmi les variétés les plus simples figurent les courbes et surfaces du plan et de l'espace euclidien. Traditionnellement définies par des équations, elles s'obtiennent toutes, au même titre que les polyèdres, à partir d'un « patron » plan et d’« instructions de collage ». C'est là le mode de définition général des variétés. |
Valeur propre, vecteur propre et espace propre En mathématiques, le concept de vecteur propre est une notion algébrique s'appliquant à une application linéaire d'un espace dans lui-même. Il correspond à l'étude des axes privilégiés, selon lesquels l'application se comporte comme une dilatation, multipliant les vecteurs par une même constante. Ce rapport de dilatation est appelé valeur propre, les vecteurs auxquels il s'applique vecteurs propres, réunis en un espace propre. La connaissance des vecteurs et valeurs propres offre une information clé sur l'application linéaire considérée. De plus, il existe de nombreux cas où cette connaissance caractérise totalement l'application linéaire. Ce concept appartient à l'origine à une branche des mathématiques appelée algèbre linéaire. Son utilisation, cependant, dépasse maintenant de loin ce cadre. Il intervient aussi bien en mathématiques pures qu'appliquées. Lire l’article |
Racine carrée de deux Il est possible que ait été le premier nombre reconnu comme irrationnel, c'est-à-dire ne pouvant être exprimé comme une fraction de nombres entiers. La découverte des nombres irrationnels est généralement attribuée à l'école de Pythagore, dont l'un des membres aurait produit la toute première démonstration d'irrationalité. Sans pouvoir affirmer avec certitude que celle-ci concernait , le fait que les propriétés de ce nombre soient connues et étudiées depuis très longtemps, et aussi qu'il est particulièrement simple d'en démontrer l'irrationalité, est un argument pour faire de « le premier irrationnel ». Le nombre intervient dans des applications de la vie courante :
|
Coordonnées polaires Les coordonnées polaires sont en mathématiques un système de coordonnées à deux dimensions dans lequel chaque point du plan est entièrement déterminé par un angle et une distance. Ce système est particulièrement utile dans les situations où la relation entre deux points est plus facile à exprimer en termes d’angle et de distance, voir par exemple le pendule. Dans ce cas, le système des coordonnées cartésiennes, plus familier, impliquerait d’utiliser des formules trigonométriques pour exprimer une telle relation. Comme il s’agit d’un système bidimensionnel, chaque point est déterminé par les coordonnées polaires, qui sont la coordonnée radiale et la coordonnée angulaire. La coordonnée radiale (souvent notée r ou ρ, et appelée rayon) exprime la distance du point à un point central appelé pôle (équivalent à l’origine des coordonnées cartésiennes). La coordonnée angulaire (également appelée angle polaire ou azimut, et souvent notée t ou θ) exprime la mesure, dans le sens trigonométrique, de l’angle entre le point et la demi-droite d’angle 0°, appelé axe polaire (équivalent à l’axe des abscisses en coordonnées cartésiennes). |
Poussée d'Archimède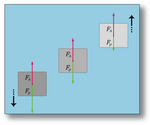 La poussée d'Archimède est une force, telle que définie par la mécanique newtonienne, qui agit sur tous les corps solides plongés dans un fluide. Pour pouvoir l'appréhender plus facilement, elle est généralement décrite par une phrase qui stipule "Tout corps plongé dans un fluide reçoit de la part de celui-ci une poussée verticale, dirigée de bas en haut, égale au poids du volume de fluide déplacé.". Cette force provient de l'augmentation de la pression du fluide avec la profondeur (effet de la gravité sur le fluide, voir l'article hydrostatique) : la pression étant plus forte sur la partie inférieure d'un objet immergé que sur sa partie supérieure, il en résulte une poussée globalement verticale orientée vers le haut. C'est à partir de cette poussée qu'on définit la flottabilité d'un corps. Cette force permet notamment aux bateaux de pouvoir flotter sur l'eau. Une légende court sur les circonstances de sa découverte: Archimède aurait eu l'intuition de cette relation alors qu'il était dans son bain en voyant son corps subir cette force, il aurait alors crié le célèbre « Eurêka ! » (j'ai trouvé !). |
Produit scalaire En mathématiques, et plus précisément en algèbre et en géométrie vectorielle, le produit scalaire est une opération algébrique s'ajoutant aux lois s'appliquant aux vecteurs. À deux vecteurs elle associe un scalaire, c'est-à-dire un nombre tel que ceux qui définissent cet espace vectoriel — réel pour un espace vectoriel réel, complexe pour un espace vectoriel complexe :
Le produit scalaire permet d'exploiter les notions de la géométrie euclidienne traditionnelle : longueurs, angles, orthogonalité en dimension deux et trois, mais aussi de les étendre à des espaces vectoriels réels de toute dimension, et aux espaces vectoriels complexes. Cette opération s'appelle « produit » en raison de certaines propriétés (distributivité sur l'addition, bilinéarité), mais il ne s'agit pas du seul produit qu'on puisse associer à deux vecteurs — voir par exemple le produit vectoriel, dont certaines propriétés sont liées au produit scalaire. |



